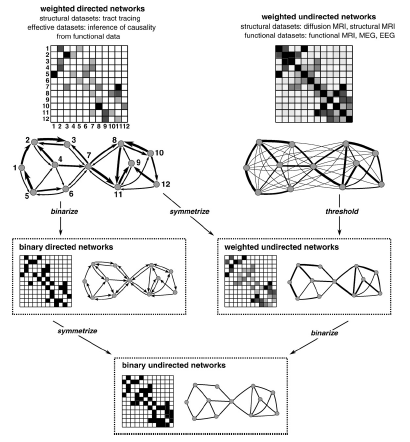
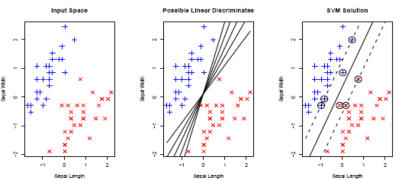
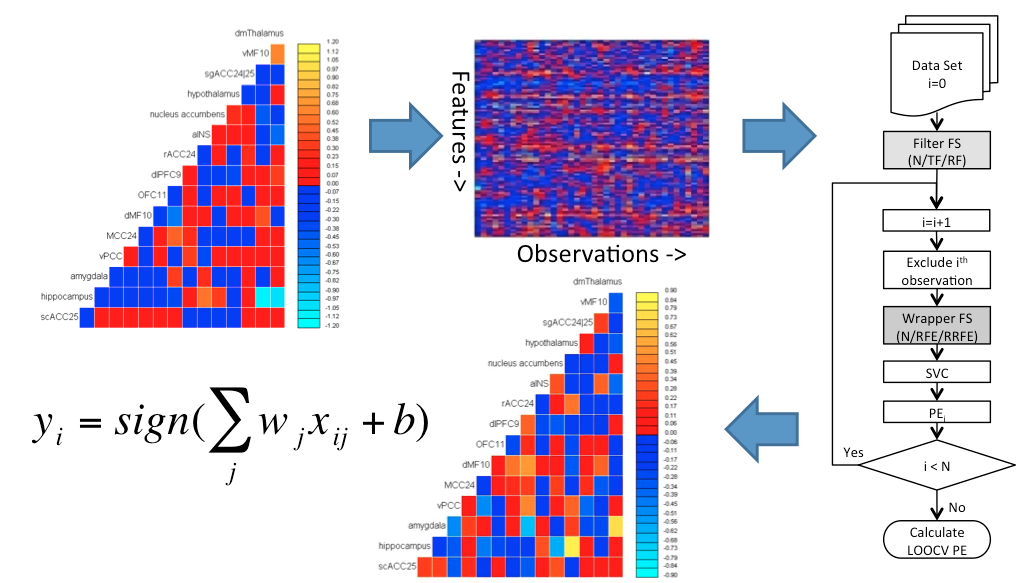
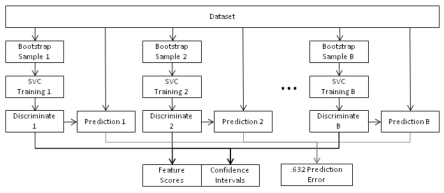
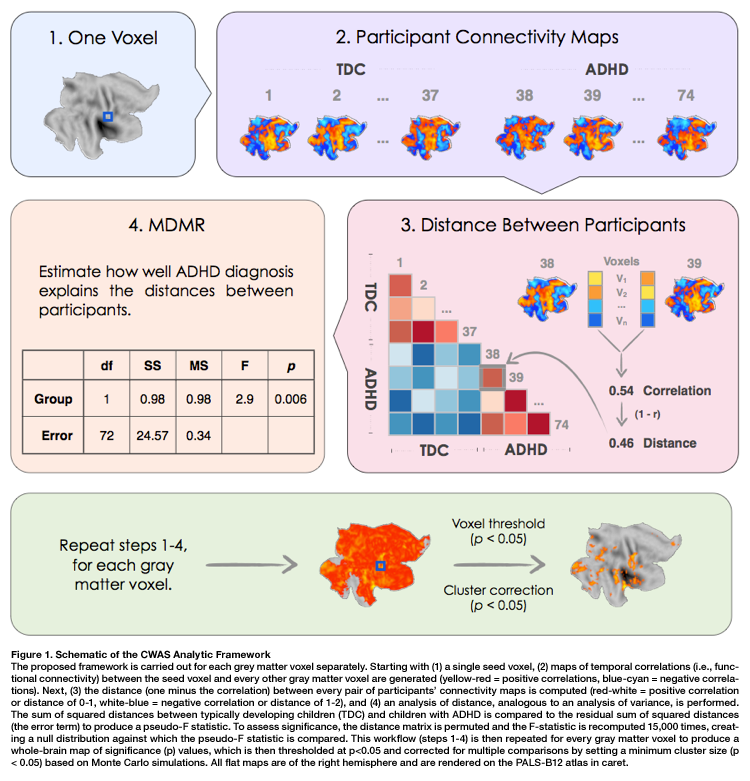
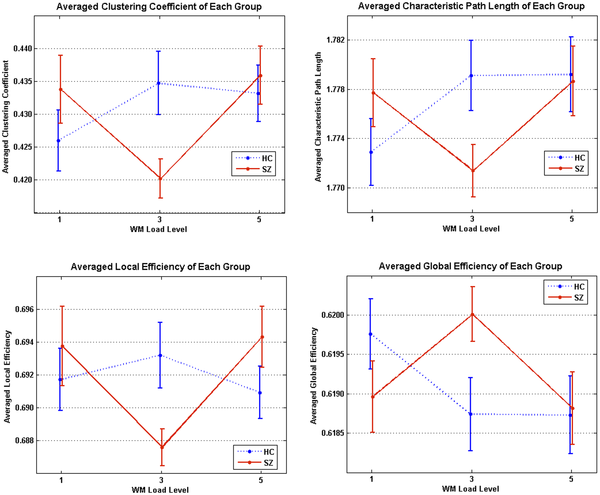
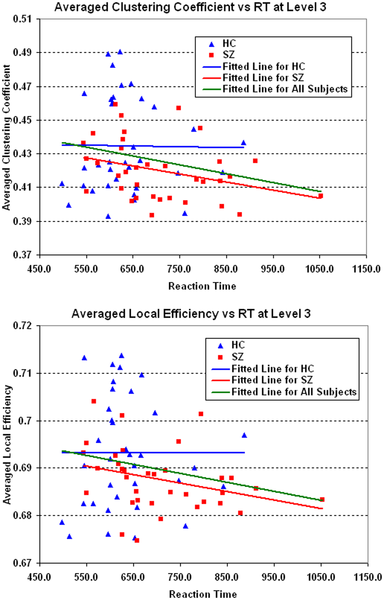
Comparing connectomes

• Once we have a connectome graphs for a set of individuals, the next challenge is comparing them
  • Indentify connections withen the graph, or subgraphs, that vary with disease state or other phenotype

What is a graph?

• Mathmatical description of the relationship between ``things''
• Consists of nodes and edges
• Nodes correspond to brain areas
• Edges correspond to connections between brain areas
  • structural connections from dMRI
  • functional interactions from fMRI
• Graphs derived from fMRI and dMRI data can be treated similarly, except for a few exceptions

Weighted and binarized

• Edges in a weighted graph are annotated with a weight that corresponds to the edge strength
• No such weighting is used with binarized graphs

A note about Thresholding

• Although, every node could be connected to every other node, this is not likely the case
• Use thresholding to remove unlikely connections due to poor strength or likelihood of error
• Thresholding is also necessary for binarizing connections
• Sparsity threshold: keep only a fraction of the strongest connections
• Significance threshold: remove edges that may have arisen by chance
• Although negative correlations can and do arise in functional connectivity, they are hard to interpret in a graph sense and are often removed

Bag of edges

• The most obvious is to perform a univariate test on each connectome of the graph
  • Allows commonly employed statistical tests such as t-tests and general linear models to be employed
• The result is a very large number of connections \(\frac{N_{vox}*(N_{vox}-1)}{2}\)
  • 19 900 connections when \(N_{vox}=200\)
• As a consequence, their will be a large number of false positives unless a control for multiple comparisons in employed
  • Bonferroni Correction, False Discovery Rate (FDR), Groupwise FDR, Network Based Statistic

Prediction Modeling

• Another option for bag of edges style analyses take into account interactions between features
• Also, estimate the significance of an identified pattern differences based on \(p(\text{disease state}|\text{pattern})\) rather than \(p(\text{pattern}|\text{NULL})\)

Classification

• Given a training set of observations and corresponding (categorical) labels, the objective is to find a linear hyperplane that is capable of seperating observations from different categories
• For linearly seperable data there are an infinite number of hyperplanes that meet this requirement
• Support Vector Classification finds the unique hyperplance that maximizes the perpendicular distance from the hyperplace to the nearest observations of a class (margin)

Train vs. Test

• Training is the process of solving a mathmatical algorithm to learn a classifier
  • Requires: Data + Labels
  • Results: Model
• Testing involves applying the classifier to a never-before-seen dataset to estimate prediction accuracy (or generalization error)
• Test and training datasets should be independent to avoid biased estimates of prediction accuracy

Bag of Edges Predictive Modeling

Feature Selection

• Filter methods: Perform a univariate test at each edge and only include those that pass a liberal threshold (univariate criterion that is not sensitive to multivariate relationships)
• Reliability Filter: Estimate bootstrap confidence intervals and exclude features whose 95% CI include zero

Connectome Wide Association Studies

Graph Invariants

• As an alternative, we can reduce the number of tests to one per node or one per graph using graph invariants (complex network measures)
• Graph invariants: a property of a graph that does not depend on the graphs represtation or orientation
• The same graph can be represented in many different ways

Node Centrality (Hubbiness)

• The relative importance of a node in a network, determined by its connections
• Degree: Number of links connected to a node
• Closeness Centrality: the average of the inverse distance from the node to all other nodes
• Betweenness Centralty: the average length of all shortest paths that pass through a node
• Eignevector: average of the centrality measures for the nodes that a target node is connected to
• Pagerank Centrality: derives a score based on the number and centrality of the nodes a target node is connected to (Google's algorithm)

Efficiency

• Efficiency is a measure of how quickly information can travel between any two nodes in a network
• Global efficiency: The average inverse shortest distance between every two points in a network
• Local efficiency: the inverse of the average shortest path connecting all neighbors of a vertex.

Small Worldness

• Small world graphs, are graphs in which nodes can be quickly reached from every other node by a small number of hops, although the number of edges between nodes is minimized
• Clustering Coefficient (C): the number links that exist between a node and its neighbors, divided by all possible links to neighboring nodes
• Characteristic Path Length (L): The average of all shortest paths in the network
• Small worldness of a network is $S=, where \(C_{rand}\) and \(L_{rand}\) are the clustering coefficient and characteristic path lengths that would have been obtained from randomly generated graphs with the same number of nodes and edges.
• if S>1.0 the graph is said to be ``small world'' which means that
  • its clustering coefficient is higher then expected from a random graph (resilient to point attacks)
  • its average path length is shorter than expected from a random graph (efficient)

Functional vs. Structural

• Since functional interactions do not imply a route or wire between connected regions, path measures don't make since for these graphs
  • i.e. the fact that A is connected to B and B is connected to C does not imply that information can travel from A to C, if A and C were where functionally connected, their activity would be correlated
• This is not the case for structural graphs

Example: Small Worldness in Schizophrenia