Leftover from fMRI lecture

• Constructing brain areas (Regions of Interests, ROIs) using clustering algorithms
• Measuring functional interactions between brain areas

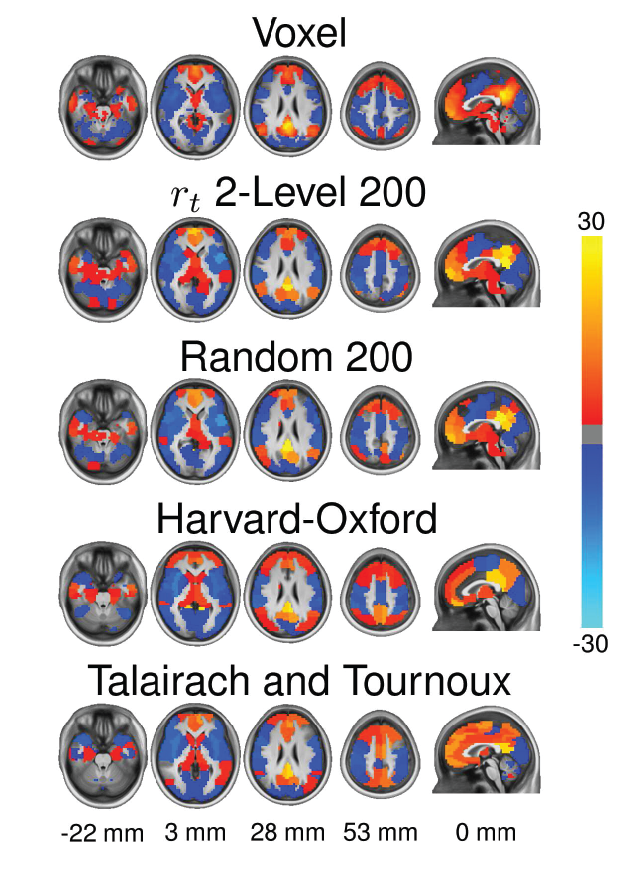
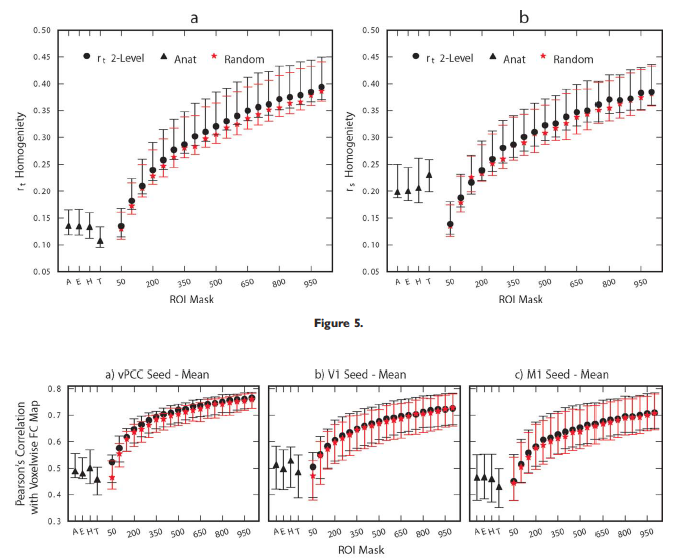
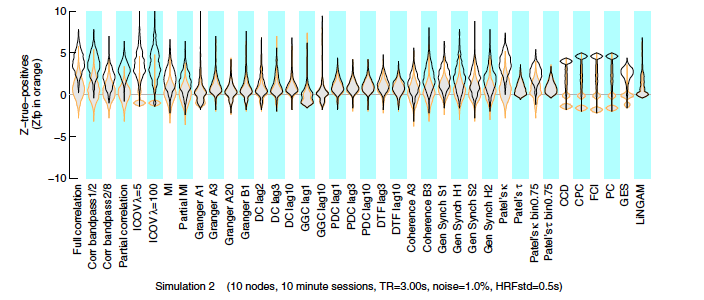
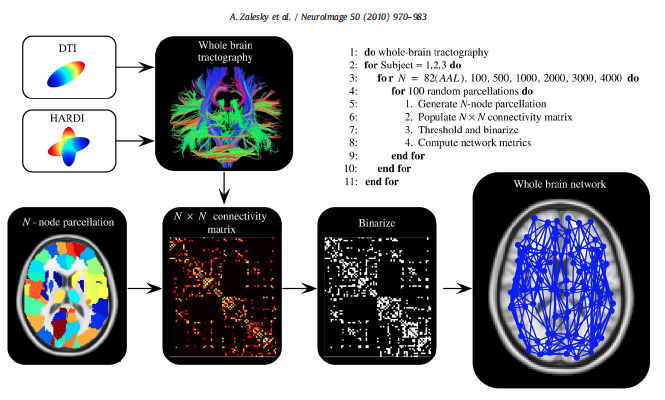
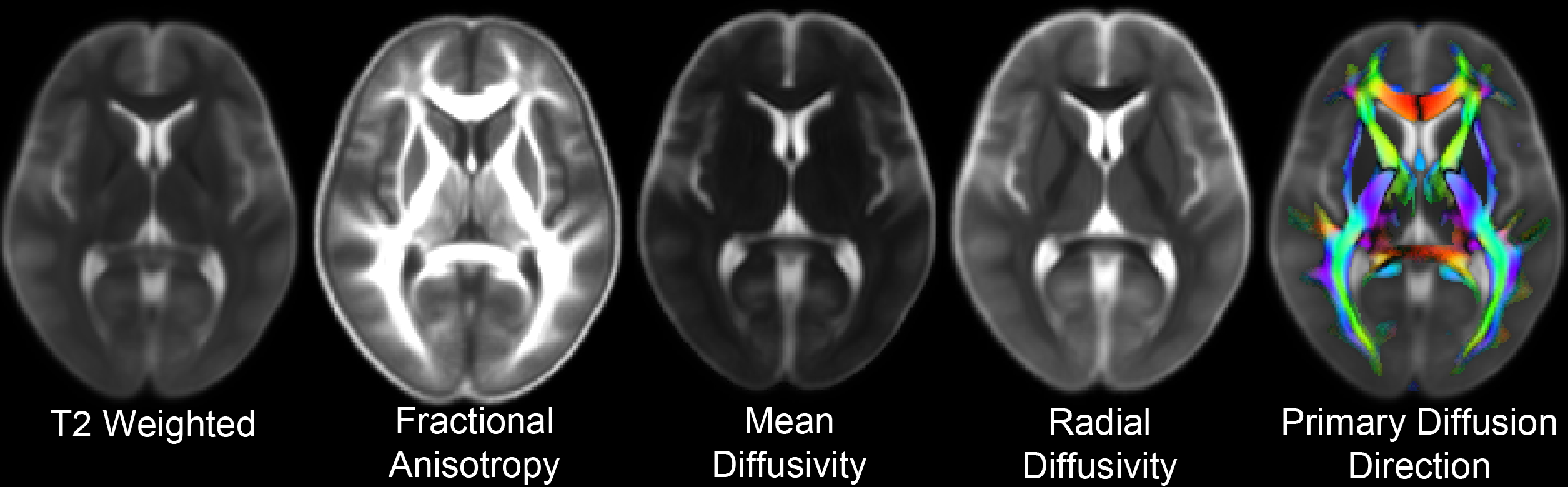
Brain Areas

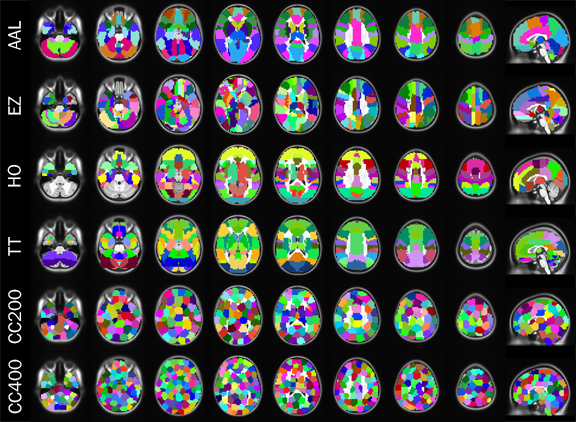
• To construct a connectome graph, you must first choose the areas to use as graph nodes
• Voxels are a logical choice, but will result in very large connectomes
• Alternatives are to use brain atlases derived from cytoarchitectonics, cortical landmarks, or from clustering data

Brain Areas

• Anatomical atlases provide good interpretability but may not accurately fit brain function
• Best to derive brain areas from the data (can be done with functional and structural data)

Clustering Brain Data

1. Preprocess the data
2. Construct affinity matrix for each dataset
   • \(N_{vox} \times N_{vox}\) matrix where each entry corresponds to the similarity of the voxel's time course (fMRI), or connectivity pattern (fMRI or dMRI)
   • Constrain connectivity to just neighboring voxels
3. Cluster individual data
   • Several different clustering algorithms can be used
4. Combine clustering solution across datasets
   • Create affinity matrix for each clustering solution, where similarity is 1 if two voxels are in the same cluster, and 0 otherwise
   • Average affinity matrices across datasets
5. Perform group level clustering
6. Determine optimal number of clusters
   • Calculate clustering solutions with different numbers of clusters
   • Compare solutions to find the best

Finding the optimal number of clusters

• Distortion index, silhouette, leave-one-out cross validation, representational accuracy
• No clear best solution, instead there is a continuum of solutions to choose from

Creating Edges

• Function interactions are typically measured using Pearson's correlation, although many other methods have been proposed \[\rho(v_i,v_j)=\frac{1}{T-1}\sum\limits_{t=0}^{T}\frac{(v_{i}[t]-\mu_{i})(v_{j}[t]-\mu_{j})}{\sigma_{i}\sigma_{j}}\]
  • \(v_i[t]\) and \(v_j[t]\) are the time courses for the \(i^{th}\) and \(j^{th}\) brain areas, respectively
  • \(T\) is the number of samples in a time course
  • \(\mu_i\) and \(\mu_j\) are the means of the \(i^{th}\) and \(j^{th}\) brain areas
  • \(\sigma_i\) and \(\sigma_j\) are the standard deviations of the \(i^{th}\) and \(j^{th}\) brain areas

Other Methods

DTI Connectomes Overview

Diffusion Tensor Imaging

Diffusion MRI

• Brian Wandell PhD' Diffusion Tutorial from NIPS